Максимон Маркова
Совершенно не ожидал увидеть частицу, по массе почти совпадающую с т.н. максимоном Маркова.
Причём, эта частица находится в первом поколении частиц, вместе с аксионом, хиггсом и d-кварком.
Только есть маленькое дополнение. Один из аргументов x дан в обратном значении.
Фактически, это та же функция x^(N^x), только "перевёрнутая".
А именно, x^(N^(1/x)).
Масса максимона Маркова
предполагается 1.2209 * 1019 GeV или 2.176 * 10-5 г.
Согласно моей трактовке, она принимает значение 1.63778 * 1019GeV
B случае, если параметр N будет равняться константе Лежандра, минус 1. Т.е. N = 0.08366...
То же значение для массы максимона Маркова получим при N = 2*s. Ну, примерно то же.
*****
Бозон Хиггса
2012-й год отметился открытием бозона Хиггса. См. здесь: ЭЛЕМЕНТЫ.
Учёный народ всё ещё осторожничает, но, по всей видимости, открытие состоялось.
Теперь, что касается меня. Мог ли я предсказать бозон Хиггса? Ведь гипотеза была заявлена в 2009 году. (Хоть и не в рецензируемом журнале, но тем не менее).
Единственное, что я мог сказать абсолютно точно, так это о некой скалярной частице, массой 0.2 MeV. И такая частица в PDG заявлена. Это так называемый "космологический аксион". Вот ЗДЕСЬ, прямо в самом начале длинного списка.
Место хиггса в данной гипотезе, как и "космологического аксиона", может быть исключительно в выражении
и ни в каком другом.
Минимум уже определен и приходится на "космологический аксион", массой 0.2 MeV.
Разумеется, массу хиггса определить было непросто. Да не то что непросто - невозможно.
Но теперь мы имеем очень небезынтересные данные.
...Но прежде, совсем немного...
Об альфе
Да-да, о той самой, "одной сто тридцадь седьмой с копейками", что называется постоянной тонкой структуры. :)
Нумерологи всего мира мозг весь изломали над приближением математического значения альфы к её физическому значению.
Известному, кстати, с довольно большой точностью.
Отметился здесь и я, грешник. :)
Так вот, говоря об этой самой альфе, совершенно невозможно пройти мимо одной ну очень интересной работы Дмитрия Волова. Собственно сама его работа (см. ЗДЕСЬ) - тема отдельного разговора. Речь о самой альфе.
У Дмитрия Волова всё описано достаточно мудрёно.
Попробую всё это дело перевести с физико-математического языка на человеческий. :)
Я даже не буду выписывать формул. Для начала посмотрите бифуркационный график обычного логистического отображения. Ну, хотя бы ЗДЕСЬ. Вы увидите древо, в котором каждая следующая ветка делится на две ветки, кадая следующаа - ещё на две и т.д.
Что сделал Дмитрий Волов. Он придумал такую формулу (чуть сложнее), когда участвует не одно древо, а два.
И эти два древа (внимание!) ВСТРЕЧАЮТСЯ СВОИМИ КРОНАМИ.
Именно, в этой формуле явно фигурирует альфа.
В оригинальной статье Дмиртий Волов говорит о неких "крысках" и "ушах крысок".
Значит, разъясняю: в качестве альфы взято физическое значение постоянной тонкой структры,
а графики выполнены в Маткаде, не располагающем своими возможностями к большой глубине исследования.
Поэтому, график показывает четырёх крысок с длинными хвостами и какими-то странными серыми ушами.
Вот, что в этих крысиных ушах творится, меня и заинтересовало.
Оказалось, что, если не упираться рогами в физическое значение п.т.с., а взять его чуть-чуть больше, то в ушах крыс явно прослеживаются ещё крысы, а у тех в ушах ещё и ещё... . Итак, эти крысы множатся, действительно, как крысы. То есть, два дерева встречаются своими кронами. При определённом значении альфы. И это значение приблизительно равно a = 0.007347748...
Что произойдёт, если мы возьмём значение чуть больше, чем a = 0.007347748?
Древо начнет обедняться. Два древа встретятся своими кронами: последняя ветка левого древа точно входит в последнюю ветку правого.
А что будет, если мы возьмём значение чуть меньше, чем a = 0.007347748?
Тогда, при встрече левого и правого древа, на стыке, вместо четких веток мы обнаружим не чёткие линии, а хаотическое расположение точек.
И лишь только, если мы будем постоянно уточнять число a, мы будем получать всё большее число встречных веток, стремящееся к бесконечности.
Итак, формула Волова даёт не одно древо, а два встречных.
Оказывается, что таких встречных пары деревьев всего две.
Вторая пара получается в случае, если a = 0.006939...
А реальное физическое значение постоянной тонкой струкутры находится между этих двух значений.
Пока ещё не доказано, что п.т.с. является динамической константой,
(а значит, и все другие физические константы), но всё идёт к тому.
Насколько нужна альфа в моей модели? Ну, если только для "оправдания" числа t. Да ещё в очень грубом приближении для определения масс нуклонов. Но, мне думается, числа Волова, то есть, крайние значения альфы, могут и должны найти своё применение.
.....
... И, самое смешное, что применение этих крайних значений альфы нашлось. :)
И нашлось оно ни где-нибудь, а именно в открытом ныне бозоне Хиггса.
Для начала покажем две картинки, взятые вот отсюда: http://elementy.ru/news/431868
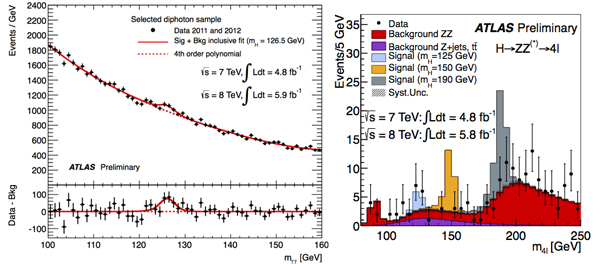
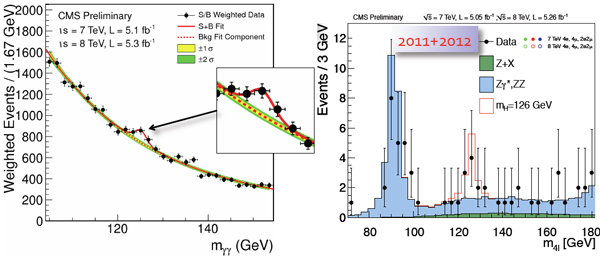
Очень небезынтересные картинки, однако.
Заметили на левых графиках небольшую "пипочку"? Этакий бугорочек...
А ведь цены нет этой "пипочке"!
Если в формулу для скалярного бозона (одну из самых простейших, кстати) (x^x)^N, где N = 1/e - a, (где e - основание натуральных логарифмов или число Непера), взять a = 0.006939 и a = 0.007347748, то есть, те значения, которые получаются из математических выкрутасов Дмитрия Волова, то значения массы такой частицы получатся, соответственно
Обнаружив Альфу у себя в полистепенных, да ещё в таком рафинированном виде, (Оказавшуюся впоследствии полнейшей чушью, кстати. (запись добавлена 17.01.2015)), я ломанулся искать оную в воловских бифуркационных графиках.
Разумеется. А что оставалось? ...И вновь даю ссылку на эту чудесную статью:
http://chaosandcorrelation.org/Chaos/DV_1_5_2012.pdf.
Цитирую: "При значении параметра a=1/137... вся хаотическая часть оказывается скрытой в “ушках крыс”".
Ох, сколько же там скрыто в этих самых "ушах крыс"!!...
Я не поленился, исследовал. Насколько мне позволила мощность моего компьютера.
Оказывается, там, в этих "ушах крыс" не так уж и всё хаотично. Там проявляются вполне себе ясно видимые закономерности.
Да что там говорить? Давайте, я вам сейчас выдам на гора два графика, вместе с текстом программы. И вы всё поймёте.
Внимательно посмотрите на эти графики.

Рис. 1
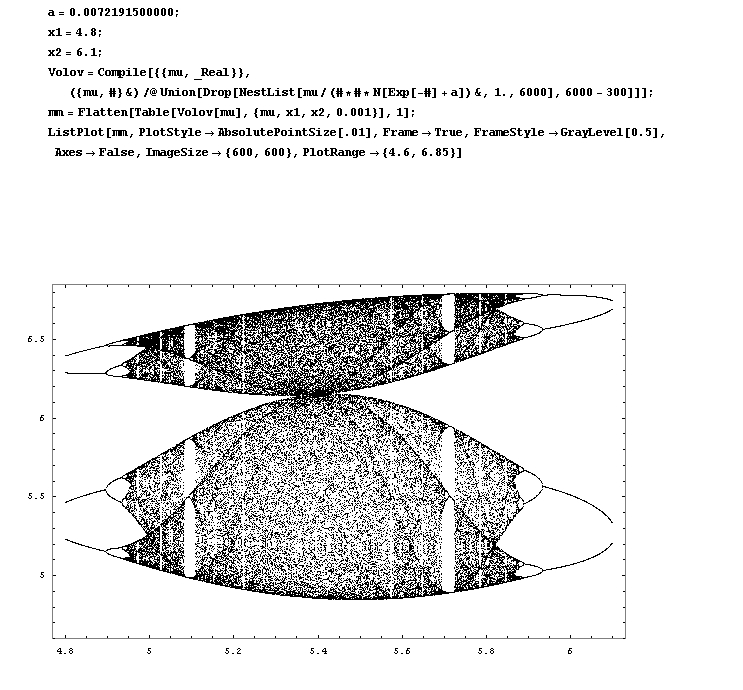
Рис. 2
Видите, на переносице у муравья что? Стыковка двух кривых. Как раз между "глаз". Если провести мысленную плавную кривую, соответствующую бифуркациям.
Ну вот. Так Альфа, в формуле Волова, то есть, "нумерологическая" Альфа, при таком условии - точной стыковке двух "ушей крыс",
(или, теперь уже не знаю, как эти кривые и называть) - приобретает значение a = 0.0072973877...
Разумеется, это число не может заменить собой реальную п.т.с. Ибо, математического значения для реального значения п.т.с. не существует.
Существует некий математический "коридор" для реальной п.т.с., в котором она и существует.
Для экспериментального значения п.т.с. кривые в переносице муравья чуть-чуть пересекаются. Самую малость, но пересекаются.
Моя же формула вряд ли покажет до такой степени точное значение Альфы, как у Волова. Она просто показывает, что есть некое чисто математическое значение, проще говоря, число, подобное константе Лежандра. И от которого нельзя отмахнуться, как от надоедливой осенней мухи. Что показывают и бифуркационные графики Волова.
Теперь перейдём от "муравья" к рисунку 2.
Здесь другая закономерность. Здесь, как видите, "крысы" соприкасаются попарно.
Причём, соприкасаются они всеми своими частями тела ("ушами" тут уже трудно назвать).
Эту точку соприкосновения нетрудно выявить. Она соответствует значению a = 0.00721915...
Что, как видите, не соответствует значению Альфа очень точно. но находится "близко".
Так вот. Именно это значение и даёт нам массу бозона Хиггса!
По моим подсчётам это значение получается приблизительно 125.779 GeV
При экспериментальном значении, по данным PDG: 125.9 +-0.4 GeV
То есть, вплоть до 6 значащих цифр можно проверять, насколько моя гипотеза не фейковая. По Хиггсу.
(: Вперёд на мины, господа-тофарисчи физики! :)
Это ещё не всё. Дело в том, что формула для Хиггса, она же и формула для космологического аксиона. Только аксион массой 0.2 MeV имеет единственное решение в рассматриваемой формуле (x^x)^N. Для Хиггса нужно искать второе значение, где N не меньше единицы, как в рассматриваемом случае, а больше единицы.
Итак, монополь Дирака. Я уже совсем расстался с мыслью его "отловить" в своём зверинце полистепенных функций. Стойкая уверенность, что монополь прячется именно за функцией x^(x^(N^N)) была. Но не было никаких "зацепок". Кроме странного минимума функции при одинаковых N.
А если они разные?...
А если разные, то, вот такая формула
Именно, при антисимметричном параметре N и получается максимум массы.
Значение максимума массы для этой частицы получается 606.638 PeV, или 606638 TeV, или 6.06638*10-11 MeV.
Теперь, уверенность, что именно эта функция и соответствует монополю Дирака, сильно возросла.
Кроме монополя, максимумы имеются ещё в двух функциях с двойным N. Это функции
x^((N^(1/x))^N) и x^(N^((1/x)^N))
Их значения, соответственно, 0.0295731 MeV и 0.0122347 MeV
Что это за частицы - совершенно без понятия. Но если взять антисимметричные параметры N, как для монополя Дирака
x^((-N^(1/x))^N) и x^(-N^((1/x)^N))
то мы имеем очень интересные графики.
Я впервые столкнулся с волной на поле положительного значения аргумента x. Ну, если не считать двойных минимумов для адронов. Хотя, это тоже, как бы, волна. Но дело-то в том, что в данных двух функциях мы видим волну бесконечную. Такую же, как в отрицательной области определения.
Это может говорить только об одном: о том, что данные частицы имеют какое-то основополагающее значение.
Это вырожденные функции, состоящие из 4-х знакомест, но содержащие всего 2 "икса". То есть, строго говоря, они, как и функция монополя Дирака, находятся в основании возникновения вещества. Как космологический аксион, хиггс, гравитон, глюон и d-кварк, невырожденных 3-х знакоместных частиц.
Не иначе, как это - гипотетические лептокварки.
Самое забавное, что массы таких частиц вычислять можно. Ибо, количество минимумов здесь конечно. То есть, при любом значении N, мы можем вычислять крайний минимум слева, наиболее близкий к началу координат. Просто, минимумы здесь переходят, так сказать, "квантово", т.е. скачком.