Владимир Привалов

Полистепенные функции и элементарные частицы

Три анкера для времени: электрон, мюон, таон

Ещё раз выпишем формулу для времени частиц.

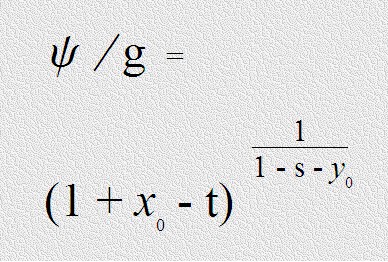
Где: x₀ и y₀ - координаты экстремума функции в интервале от 0 до 1. S - число Шакти.
t - число времени, приблизительно равное 0.232142. Взято оно из функции фотона (xx)(xN), единственной относительно простой полистепенной функции, график которой "симметричен" относительно единицы. Подробнее см. число, близкое к p.
g = 2*10^-43 - специальный коэффициент, обеспечивающий привязку к времени жизни лептонов.

Значения времени жизни для трёх базовых лептонов:
электрон    > 4.6 * 10²⁶ лет, или 6.0444 * 10³² c

мюон          = 2.197034 * 10^-6 c

таон            = 290.6 * 10^-15 c

"Частица с шириной распада 1 эВ имеет время жизни 6.58211889(26)*10^-16 с. Напротив, квантовомеханическое состояние с временем жизни 1 с имеет ширину 4.13566733(10)*10^-15 эВ".
(dic.academic.ru)

Ширина рспада для трёх базовых лептонов:
электрон    = 6.84215 * 10^-48 eV

мюон          = 1.88239 * 10^-9 eV

таон            = 0.0142315 eV

Именно к этим значениям будем "привязываться" "по образу и подобию", как это сделано в случае массы покоя частиц.
Здесь, правда, возникает некоторая трудность с точностью "привязки", так как значение времени жизни электрона определено очень приблизительно ( > 4.6 * 10²⁶ лет ). И, тем не менее.

Функции лептонов, разумеется, те же (иначе и быть не может)
(xx)(xN)

(x(x(xx)))(xN)

(x(x(x(x(xx)))))(xN)

...

и т.д.

Теперь, что касается коэфициента смещения g, без которого привязка к тройке лептонов по экспериментальным данным времени жизни не представляется возможной.

Для такого числа g = 2*10^-43 никакого другого объяснения, как безразмерная константа гравитационного взаимодействия (взятая здесь), я не придумал.
Величина этой безразмерной константы примерно равна 5.907 * 10^-39
Ясное дело, точность тут явно подкачала. Несмотря на явную неопределённость времени жизни электрона. Но других чисел нет и не предвидится. Так или иначе, вопрос по коэффициенту смещения g остаёься открытым.

Следует также сказать и о параметре N, включенных в каждую формулу конкретной частицы.
Здесь параметр N очень жестко однозначен и равен 1/2. Ни больше ни меньше. Шаг влево шаг вправо - побег. Удивительно, но это так.

*****

24 : 03 : 2011

Итак, возникла трудность с точностью привязки к группе руководящих лептонов (электрон, мюон, таон). То есть, ширину распада мюона и таона мы знаем более-менее точно, но вот распавшегося на запчасти электрона никто ещё в глаза не видывал.
Неожиданно открывшиеся уточнения для привязки к векторным (W и Z) бозонам позволили значительно усилить идею временного анкера. И если в старой версии программы привязка была на уровне "три шапки вправо - два пальца вниз", то теперь привязка осуществлена для мюона и таона внутри допустимых экспериментальных отклонений (PDG).
Что касается векторных бозонов, то - да, они не попали в допустимые экспериментальные отклонения PDG. Ho!

Но вот их значения, следующие из программы:
для W -- 1.496 GeV
при экспериментальных от 1.994 GeV до 2.279 GeV
для Z -- 1.7418 GeV
при экспериментальных от 2.4931 GeV до 2.4975 GeV

А вот коэффициенты:
для привязки к лептонам -- (1-s)/E
для привязки к W-бозону -- (s+1)/2
для привязки к Z-бозону -- (s+1)/E

И у меня просто не поднялась рука подбирать к ним какие-либо уточняющие навороты. :)

А вот уйти от параметра N, строжайше равного 1/2, пришлось. В противном случае ширина распада мюона и таона никак не хотела ложиться в прокрустово ложе PDG.
Параметр N будет следующим:

N = 1/2 + (-ln cos(1/a)-1-x)

Но это число x (в программе это переменная "ni"), равное 8.123..*10^-6 очень сильно смахивает на безразмерную константу слабых взаимодейсвий (1.0*10^-5).

Кроме того, уточнился параметр g = 7.1320...*10^-44 (в программе "r"), который я по-прежнему склонен считать чем-то очень похожим на безразмерную гравитационную константу.

Значение для времени жизни электрона, при всех этих выкрутасах получается:
1.472047 * 10²⁵ секунд.
Или 4.6678 * 10¹⁷ лет.

Ну и ещё кое-что о привязке к "электронвольтам".
В данном случае просто численно привязываемся к таону и мюону. Будем считать, для простоты, что у нас значения по мюону и таону просто совпали с реальными значениями в электронвольтах. Короче, примем как данное, что ширина распада таона примерно равна 0.014183 электронвольт.

Ну и к словам, я добавляю (: нет, не быка :) программу, только что написанную мною. :)

pa3 = 250;
s = 0.0416872367002117273721536029316450472170048623250488650352055324746280405044354524475842838820374;
L = 0.0836592127750214236278814859093986743178339020813267535222382992297614130733153618706356269226574;
q = 2.3580931451190032144887737391890350539639469479342461630290060725949906550191572682206868865486755;
a = 0.0072973526572966465259127085759337793837912120338450931986466869424786785379739846203834368546851;
p = L - 2*s;
ah = 1/a;
La = N[-Log[Cos[ah]], 150];
Print["Получение числа t=0.2321420..."];
Nt = 0.6732159718396782190271378926182524154468000473166717838156742337048390671516104399000000000000000;
f[x_] := N[(x^x)^(Nt^x), 150];
a1 = 0.3000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.3300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xm = a2; ym = f2;
(* Max *)
f[x_] := N[(x^x)^(Nt^x), 150];
a1 = 4.240000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 4.280000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 < f2, f2 < f3], {a1 = a2}];
If[And[f7 < f6, f6 < f5], {a7 = a6}],
{pa3}]
Ti = a2; ym1 = f2;
Print["======================================================================================="];
Print[Ti];
Print[1/xm];
Print[ym1];
Print["---------------------------------------------------------------------------------------"];
Print["Pазность двух экстремумов одной функции фотона (xx)(Nx)"];
Print[ym1 - 1/xm];
T = Ti + s - N[(a*(1 - s))/E, 150];
t = 1/T;
r = 7.1320000000000000000000000000000000000000*10^(-44);
ni = 8.123000000000000000000000000000000000000*10^(-6);
(* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^*)
No = 1/2 + (La - 1 - ni);
(* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ *)
Print["Здесь коэффициенты перевода времени жизни в ширину распада (в электронвольтах) и обратно."]
tt = 6.5821188900000000000000000000000000000000000*10^(-16);
J = 4.135667330000000000000000000000000000000000000*10^(-15);
(* 1 эВ = 6.5 ___ 1 c = 4.1 *)
mul = 2.197055000000000000000000000000000000000000*10^(-6);
Muu = N[2*Pi*tt/mul, 35];
Print["Ширина Mu max = ", Muu]
mur = 2.197023000000000000000000000000000000000000*10^(-6);
Mud = N[2*Pi*tt/mur, 35];
Print["Ширина Mu min = ", Mud]
Ta = 291.6000000000000000000000000000000000000000*10^(-15);
Tao = N[2*Pi*tt/Ta, 20];
Print["Ширина Ta max = ", Tao]
Ta = 289.6000000000000000000000000000000000000000*10^(-15);
Tao = N[2*Pi*tt/Ta, 20];
Print["Ширина Ta min = ", Tao]
(* В данном случае просто численно привязываемся к таону и мюону. *)
(* Будем считать, для простоты, что у нас значения по мюону и таону *)
(* Просто совпали с реальными значениями в электронвольтах. *)
(* Короче, примем как данное, что ширина распада таона *)
(* Примерно равна 0.014183 электронвольт *)
el1 = 4.60000000000000000000000000000000000000000*10^(26);
el1 = el1*365*24*60*60;
ell = N[2*Pi*tt/el1, 20];
Print["Ширина El = ", ell, " eV"]
Print["Ширина El = ", ell/1000000, " MeV"];
(* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ *)
f[x_] := N[(x^x)^(x^p), 150];
a1 = 0.200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xi = a2; yi = f2;
(* _______________________ *)
v := N[((1 + x0) + s)^(1/(1 - y0)), 150];
(* _______________________ *)
y0 = yi; x0 = xi;
ew = N[(v^v)^(v^p), 150];
(* ---------------------------- *)
f[x_] := N[(x^x)^(x^No), 150];
a1 = 0.2000000000000000000000000000000000000;
a7 = 0.7000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{150}]
xe = a2; ye = f2;
f[x_] := N[(x^(x^(x^x)))^(x^No), 150];
a1 = 0.200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xm = a2; ym = f2;
f[x_] := N[(x^(x^(x^(x^(x^x)))))^(x^No), 150];
a1 = 0.200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xt = a2; yt = f2;
Nw = N[E^(Pi - a*(s + 1)/2), 150];
f[x_] := N[(x^x)^(Nw^x), 150];
a1 = 0.100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xw = a2;
yw = f2;
Nz = N[E^(Pi - a*(s + 1)/E), 150];
f[x_] := N[(x^x)^(Nz^x), 150];
a1 = 0.100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
a7 = 0.800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{pa3}]
xz = a2;
yz = f2;
(* _______________________ *)
x := N[((1 - t) + x0)^(1/((1 - s) - y0)), 150];
(* _______________________ *)
y0 = ye; x0 = xe;
el0 = N[(x^x)^(x^No), 150];
y0 = ym; x0 = xm;
mu0 = N[(x^(x^(x^x)))^(x^No), 150];
y0 = yt; x0 = xt;
ta0 = N[(x^(x^(x^(x^(x^x)))))^(x^No), 150];
el = el0/ew;
mu = mu0/ew;
ta = ta0/ew;
Print["Экспериментальные данные eV"];
Print["El = 2.850894540108558388 * 10(-49)"];
Print["El = ", el*r];
Print["Время El = ", J/(el*r), " cek"];
Print["Время El = ", (J/(el*r))/(365*24*60*60), " лет"];
Print["========================"];
Print["Max = 1.882368566092210198295376271 * 10(-9)"];
Print["Muon = ", mu*r];
Print["Max = 1.882395983098820939615037218 * 10(-9)"];
Print["========================"];
Print["Max = 0.01418267239360672454"];
Print["Taon = ", ta*r];
Print["Min = 0.01428061902615925717"];
Print["========================"];
y0 = yw; x0 = xw;
www = N[(x^x)^(Nw^x), 150];
w = www/ew;
y0 = yz; x0 = xz;
zzz = N[(x^x)^(Nz^x), 150];
z = zzz/ew;
Print["Max = 2.279 GeV CERN PDG"];
Print["W GeV = ", w*r*10^(-9)];
Print["Min = 1.994 GeV Tevatron PDG"];
Print[" "];
Print["Max = 2.4975 GeV"];
Print["Z GeV = ", z*r*10^(-9)]
Print["Min = 2.4931 GeV"];

Старую программу удалять не буду. Именно потому, что в старой программе наличествует ошибка в виде совершенно лишней переменной ev=0.51099.
Эта переменная вошла, как троянский конь, по инерции (мЫшленья), поскольку все вычисления по массам частиц производились по отношению к массе электрона в МэВ'ах.

Раньше, говорят, все научные труды писались только в стихах. Не в стихах не принимались. Как теперь не принимаются, если не прошли некоего Помазанного Рецензента. :)

t = 0.232142036766647050549206710449359530;
s = 0.041687236700211727372153602931645047217;
ev = 0.51099891000000000000000000000000000;
ew = 30.1567498951464687327772000000000000;
J = 4.13566733000000000000*10^(-15);
No = 1/2;
Print["__________________________________"];
f[x_] := N[(x^x)^(x^No), 35];
a1 = 0.2000000000000000000000000000000000;
a7 = 0.7000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{150}]
xe = a2; ye = f2;
f[x_] := N[(x^(x^(x^x)))^(x^No), 35];
a1 = 0.2000000000000000000000000000000000;
a7 = 0.7000000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{150}]
xm = a2; ym = f2;
f[x_] := N[(x^(x^(x^(x^(x^x)))))^(x^No), 35];
a1 = 0.200000000000000000000000000000000;
a7 = 0.700000000000000000000000000000000;
Do[
pa = a7 - a1; d = pa/7;
a2 = a1 + d; a6 = a7 - d;
f1 = f[a1]; f2 = f[a1 + d]; f3 = f[a1 + 2*d];
f7 = f[a7]; f6 = f[a7 - d]; f5 = f[a7 - 2*d];
If[And[f1 > f2, f2 > f3], {a1 = a2}];
If[And[f7 > f6, f6 > f5], {a7 = a6}],
{150}]
xt = a2; yt = f2;
Print["===================================="];
(* _______________________ *)
x := N[((1 - t) + x0)^(1/(1 - s - y0)), 35];
(* _______________________ *)
y0 = ye; x0 = xe;
el0 = (x^x)^(x^No);
y0 = ym; x0 = xm;
mu0 = (x^(x^(x^x)))^(x^No);
y0 = yt; x0 = xt;
ta0 = (x^(x^(x^(x^(x^x)))))^(x^No);
el = el0/ew;
mu = mu0/ew;
ta = ta0/ew;
Print["El = ", el*ev];
Print["Muon = ", mu*ev];
Print["Taon = ", ta*ev];
Print["_______________________"]
Print["M/E = ", mu/el];
Print["T/M = ", ta/mu];
Print["_______________________"]
a = mu/el; b = ta/mu;
Print[a/b]
Print["_______________________"]
Print["Экспериментальные данные eV"];
Print["El = 8.99058 * 10(-42)"];
Print["Muon = 1.88239 * 10(-9)"];
Print["Taon = 0.0142315"];
Print["_______________________"]
r = 2*10^(-43);
Print["El = ", el*ev*r]
Print["Muon = ", mu*ev*r];
Print["Taon = ", ta*ev*r];
Print["_______________________"]
Print["El = ", J/(el*ev*r)]
Print["Muon = ", J/(mu*ev*r)];
Print["Taon = ", J/(ta*ev*r)];
Print["_______________________"]
Print["M/E = ", (1.88239*10^(-9))/(8.99058*10^(-42))];
Print["T/M = ", 0.0142315/(1.88239*10^(-9))];

Здесь, в формуле времени, есть ещё одно отличие от формулы масс, о котором нельзя умолчать. Это так называетмя "фотонная поправка".
При вычислении будь то массы покоя частицы или ширины её распада (это не важно), при данных константах, получается некая "масса" электрона в абсолютных единицах, ничем не связанных с физическими. Величина эта - 30.156749895....
Так вот, при вычислении энергии низкочастотных фотонов, получались отрицательные значения. Чтобы от них уйти, пришлось ввести минус единицу как для электрона, так и для вычисляемой частицы.
Здесь же, в случае с формулой времени, такая поправка оказалась не нужна.

Далее: Число времени