Владимир Привалов

Полистепенные функции и элементарные частицы

Элементарные частицы как элементарные функции

Периодическая система элементарных частиц

• Почему нет?
• Вакуум
• Первое поколение
• Фермионы
• u-Кварк
• d-Кварк
• Электрон
• Нейтрино
• Бозоны
• W,Z-бозоны
• Фотон
• Глюон
• Глюино и голдстино
• Голдстоун
• Лептокварки
• Монополь Дирака
• Максимон
• Гравитон
• Гравитино
• Хиггсовый бозон

Почему нет?

Почему элементарные частицы нельзя представлять в виде полистепенных функций? Можно попробовать это сделать. Почему нет? При этом, следует заметить, что такие функции уравнениями движения не являются: просто они служат математической моделью, симметрией, которую мы пытаемся сопоставить окружающему нас реальному миру.

Что такое полистепенная функция? Полистепенная функция есть функция, представленная множеством аргументов, связанных между собой исключительно операцией возведения в степень.

Поскольку полистепенные функции используют только операцию возведения в степень, то и форму записи функций будем использовать сокращенную, без символов возведения в степень.

Так например, функция y = x^x запишется, как y = xx, a функция y = x^(xx), запишется, как y = x(xx). По умолчанию, принято использовать отсутствие символа действия за действие произведение. В нашем случае - возведение в степень.

Область определения и область изменения - поле положительных действительных чисел. Графики функций достаточно рассматривать в областях от 0 до 1, и от 1 до бесконечности.

Введем следующий постулат:
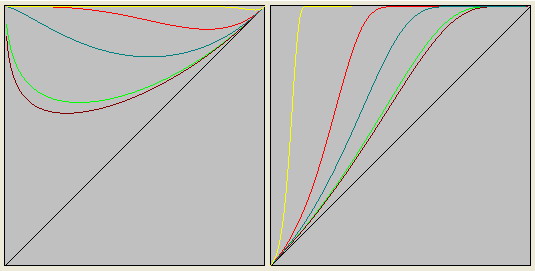
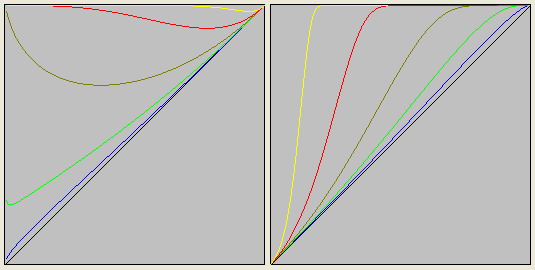
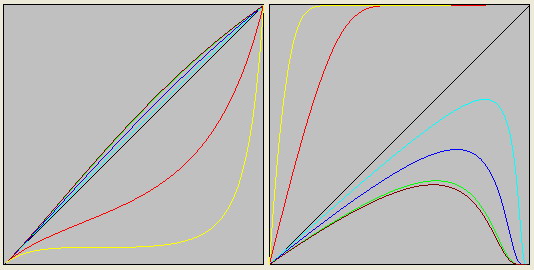
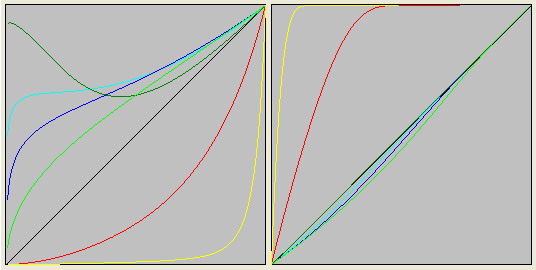
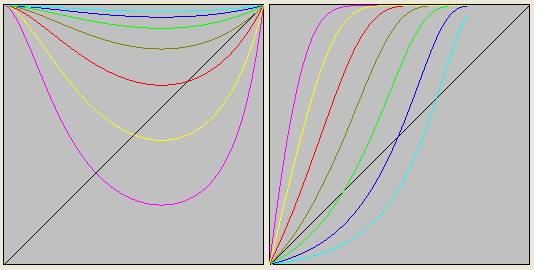
Каждой элементарной частице ставится в соответствие не отдельная полистепенная функция, а бесконечный континуум функций, рожденный определенной функцией.

Возьмем, например, функцию y = x(xx). Тогда это будет набор функций с некоторой константой N, скажем, y = x(xN). Изменяя константу N, мы получим набор, характерный для данной элементарной частицы.

Весь набор нет нужды рисовать. Достаточно отобразить несколько функций, чтобы стало понятно, какими свойствами обладает данная элементарная частица.

Условимся отображать функции
• при N=1 - оливковым
• при N=a>1 - красным
• при N=b>a - желтым
• при N=c>b - сиреневым
• при N=a<1 - зеленым
• при N=b<a - синим
• при N=c<b - голубым
• дополнительные - тёмно-зелёным и пурпурным
• граничная - белым или тёмно-красным цветом.

Мы рассматриваем вариации с одной и двумя константами N для первго поколения. Частицы с тремя константами являются вариациями вакуума.

Смею заметить, речь идет об элементарных, (подчеркиваю: истинно элементарных), частицах. Речь здесь не идет ни о протонах, ни о нейтронах, ни о мезонах, ни о резонансах... Составные частицы полистепенными функциями не отображаются.

к началу страницы

 

Вакуум

y = xN

Так выглядит знакомая всем парабола y = x^N. В левом квадрате располагаются все кривые со значениями аргумента и функции от 0 до 1. В правом квадрате - от 1 до бесконечности. Правда, правая часть слегка изменена: бесконечность перенесена в двойку.

Можно представить те же функции и в другом виде, например, используя логарифмическую шкалу. Тогда вы получите эти функции в виде прямых линий.

Что означают эти линии? Не означают ли они энергетические уровни, которые соответствуют тем инерциальным системам, в которых и находятся в состоянии покоя те или иные частицы?

Так выглядит вакуум. Является ли он частицей, как и все другие частицы? - сложный вопрос. Что, собственно, есть частица, как не флуктуация вакуума?

Можно сделать попытку представить континуум функций y = xN, как бесконечное множество инерциальных систем отсчета.

Чтобы отобразить ту или иную частицу в той или иной системе отсчета, надо в соответствующей этой частице функции вместо x подставить xL, где L - константа, соответствующая ИСО.

Предполагается ещё один тип вакуума, образованный функцией y = N. Будем называть это струнным вакуумом. Именно в такую функцию вырождается жесткий фотон.

к началу страницы

 

Первое поколение

Функция вакуума содержит в себе два элемента: агрумент x и константу N. К первому поколению элементарных частиц относятся функции, содержащие в себе три или четыре элемента.

Перечислим функции, содержащиеся в первой части первого поколения. Их всего шесть.

y = (xx)N y = (xN)x y = x(xN) y = x(Nx) y = x(NN) y = (xN)N

Две из них { y = (xx)N и y = (xN)x } фактически вырождаются в одну (графики их совпадают), а две { y = (xN)N и y = x(NN) } представляют вариации вакуума. Таким образом, первая часть первого поколения элементарных частиц представлена только тремя функциями.

Ко второй части первого поколения относятся функции с тремя аргументами + константа. Всего их 15.

((xx)x)N	((xx)N)x	((xN)x)x
x(x(xN))	x(x(Nx))	x(N(xx))
(xx)(xN)	(xx)(Nx)	(xN)(xx)
(x(xx))N	(x(xN))x	(x(Nx))x
x((xx)N)	x((xN)x)	x((Nx)x)

А также, функции с двумя аргументами + две константы.

((xx)N)N	((xN)x)N	((xN)N)x
x(x(NN))	x(N(xN))	x(N(Nx))
(xx)(NN)	(xN)(xN)	(xN)(Nx)
(x(xN))N	(x(Nx))N	(x(NN))x
x((xN)N)	x((Nx)N)	x((NN)x)

Плюс, шесть вакуумных функций: ((xN)N)N, x(N(NN)), (x(NN))N, x((NN)N), (xN)(NN), xN.

Всего 42 функции в первом поколении, представляющие собой весь известный набор истинно элементарных частиц.

Сделаем попытку толкования их свойств

к началу страницы

 

Фермионы

Фермионы-частицы, как известно, имеют полуцелый спин. Фермионы-функции характеризуются тем, что их графики в обоих частях занимают только верхние треугольники, ограниченные снизу центральной вакуумной функцией y = x, т.е. заполняют половину пространства.

Что касается гравитино (спин 3/2), то его функция также имеет похожие ограничения. Но в этих ограничениях она мало чем отличается от его логического собрата гравитона, представляющего собой тензорную частицу (спин 2).

к началу страницы

 

u-Кварк

y = x(xN)

u-Кварк - верхний кварк, частица, имеющая массу покоя. Это факт выражается в том, что функция имеет экстремум в левой части графика. Чем экстремум функции ближе к 1, тем больше масса частицы и наоборот. Энергия частицы также характеризуется величиной отклонения графика функции от вакуумной в правой части.

Характер кривой говорит о многом: масса и все виды зарядов - всё заключено в ней.

В своём нижнем энергетическом уровне кварк стремится к вакууму, и, что отличает его от вакуума, так это петля в левой части, обеспечивающая начало функции в точке (0, 1).

к началу страницы

 

d-Кварк

y = x(x(Nx))

d-Кварк - нижний кварк. Почти идентичен верхнему кварку. Отличие в том, что в d-кварке экстремум, при возрастании массы, распадается на два антиэкстремума. Это хорошо видно на графике по сиреневой линии.

О чем говорит сей факт? Не о том ли, что здесь проявляется свойство нижнего кварка иметь электрический заряд вдвое меньший, чем у верхнего кварка?

Здесь первое противоречие (: как будто их нет в других гипотезах :). d-Кварк является как бы составной частицей, ибо распадается на u-Кварк, электрон и электронное антинейтрино. Но ведь признают же кварки за истинно элементарнные частицы. Будем и мы признавать.

к началу страницы

 

Электрон

y = (xx)(xN), y = (x(xN))x

Электрон. Удивительная функция, которую нельзя рассматривать отдельно от функции нейтрино. Обратите внимание на белую кривую. Это функция - разделительная полоса, демаркационная линия. Всё, что выше её в левой части - принадлежит электрону. Электрон имеет массу покоя, причем, истинную массу покоя, т.е. такую, которая при любых условиях не может быть ниже определенной. И границу эту определяет демаркационная линия функции y = xx.

Предполагается, что масса электрона имеет значение, определяемое экстремумом функции xx - крайнего значения, при "покоящемся" электроне.

При сообщении электрону дополнительной энергии, его функция "сдвигается" на L

y = ((xL)(xL))((xL)N)

Сам этот электрон, с измененной энергией, в своей системе отсчета так и будет выглядеть, как будто бы сдвига по L и не существовало. Но по отношению к "наблюдателю" из стартовой системы отсчета, он (точнее, его функция) должен быть трансформирован. Вместо сдвига по L должен быть сдвиг по N. А сдвиг по N, как раз и говорит об изменении массы частицы, при сообщении ей дополнительной энергии в релятивистском случае.

В своей же системе отсчета "местный наблюдатель" увеличения массы не заметит.

Величина L говорит только о наличии другой системы отсчета. А наличие иной системы отсчета говорит только о том, что частицы в этих системах друг с другом никак не взаимодействуют.
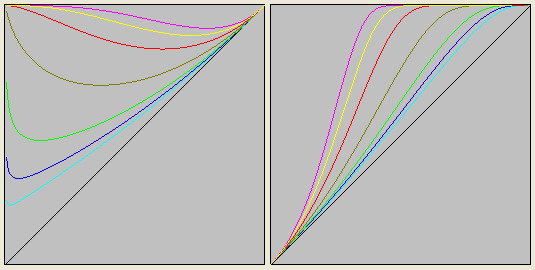
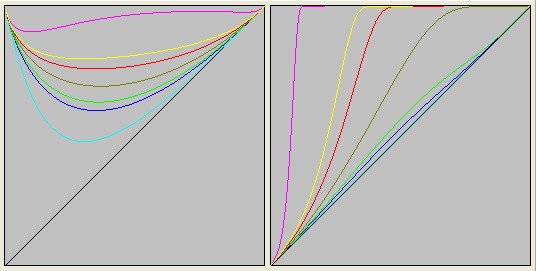
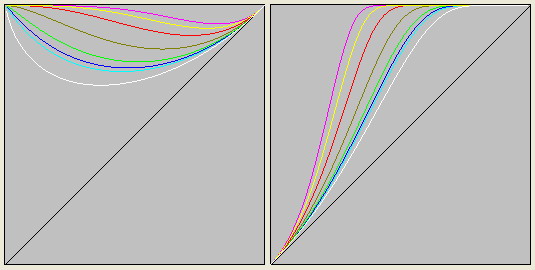
Но если они взаимодействуют каким-либо образом, то можно говорить только об единой инерциальной системе отсчета, где величина L должна быть трансформирована в величину N, что и обеспечит релятивистское изменение массы.

к началу страницы

 

Нейтрино

y = x(x(xN))

А теперь взгляните на график нейтрино. При увеличении энергии, его верхняя граница (в левой части) стремится к нижней границе электрона. Реально ощущается, что электрон и нейтрино имеют общие корни, лептонные.

Здесь нельзя обойти молчанием следующий важнейший факт: нейтрино, при увеличении энергии приобретает экстремум и антиэкстремум. Имеет ли нейтрино массу покоя или не имеет, ведутся споры. А пока они ведутся, заметим следующее: нейтрино имеет стартовую точку в левой части (0, 0), а значит, действительной массы иметь не может. Но наличие экстремума и антиэкстремума может как-то влиять на свойства нейтрино, имеющего высокие энергии.

Нельзя обойти молчанием также и тот факт, что, в случае нейтрино, в левой и правой частях, при изменении энергии происходят взаимоисключающие отклонения. Т.е., фиктивная масса нейтрино растет, но его кривая в правой части приближается к минимуму y = xx, и наоборот. Этот факт также вносит свою долю в "неуловимость" нейтрино.

к началу страницы

 

Бозоны

Бозоны-частицы имеют целый спин (0, 1, 2, ...).
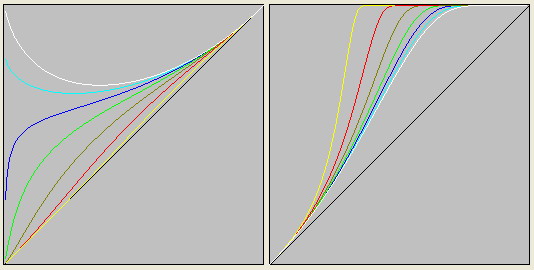
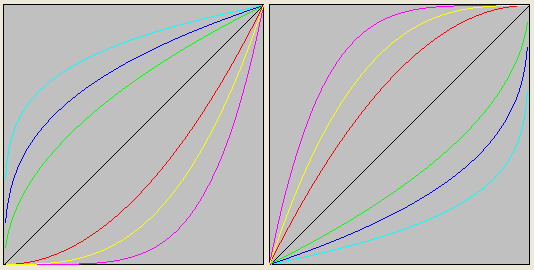
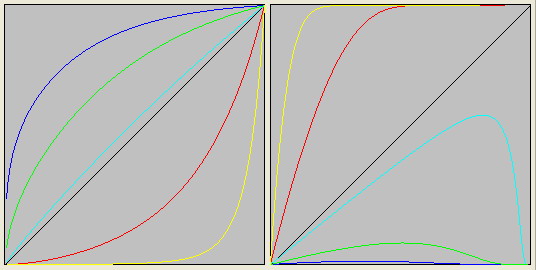
Бозоны-функции характеризуются тем, что их графики занимают всё пространство.
Но бозоны-функции делятся на две группы: векторные и скалярные.
Для скалярных бозонов характерно то, что их графики функций по аргументу и по функции начинаются в левой части и заканчиваются в правой в одной точке.
Не так дело обстоит с векторными бозонами. В левой части график их функции имееет одну точку, но в правой части, в зависимости от N, функция может прийти как в точку (oo, oo), так и в точку (oo, 1).

Для векторных бозонов характерно следующее. Как известно, они являются переносчиками взаимодействий. Фермион заполняет верхние треугольники. Незаполненными остаются нижние. Соответствующие фермионам векторные бозоны, заполняют недостающие поля. Например, для электрона точно подходит фотон. Правда его поля подходят для заполнения порознь.

Треугольники векторных бозонов располагаются крест-накрест, образуя как бы два варианта одной и той же частицы. Один из вариантов обязательно имеет массу. Так например, фотон массы не имеет, но известно, что существет т.н. виртуальный трехкомпонентный фотон, он как раз и снабжен массой.

к началу страницы

 

W, Z - бозоны

Z - бозон

y = x(Nx)

Z-бозон. Здесь добавлены дополнительные графики: x(0.9^x) - темно-зеленый и x(50^x) - пурпурный. Они приведены для иллюстрации заполнения пространства.

Обратите внимание на то, как заполняется пространство, особенно, в правой части. Векторный бозон как бы состоит одновременно из двух частей. Эти части, как и в случае фермионов, заполняют треугольники. Здесь различие в том, что эти треугольники заполняются "по диагонали", т.е. если в левой части это верхний треугольник, то в правой - нижний.

W - бозон

y = x((Nx)x)

W-бозон. Как и Z-бозон, он имеет те же свойства, только более выражены их массы: реальная (в правой части) и фиктивная (в левой части).

Характер фиктивной массы говорит о том, что эти две функции с большим правом можно считать родственными. Он же говорит о том, что эти функции являются "антиподами" пары лептокварков.

к началу страницы

 

Фотон

y = (xx)(Nx) = (x(Nx))x

Ядро всей идеи сопоставления функций элементарным частицам.

Фотон, как и все другие векторные бозоны, состоит из двух частей, крест-накрест соединенных треугольников заполнения. Справедливости ради, следует заметить, что "функция-разделитель" здесь не y = x, а y = xx, следовательно, для фотона, области заполнения не являются треугольниками.

Функция фотона - единственная функция, асимптотически приближающаяся к "струне вакуума". Речь идет о том, что функция фотона - единственная функция, начинающаяся в точке (0, 1) и заканчивающаяся в точке (oo, 1), т.е. при N --> oo функция фотона приближается к y = Const.

Но фотон не имеет массы покоя. Нам остается предположить, что частица имеет массу покоя тогда и только тогда, когда её экстремум имеется только в одной части пары противоположных треугольников. В случае, если экстремум имеется в обоих частях, массы аннулируются.

Таким образом, реальный фотон, представленный одной парой треугольников, массы не имеет. Но в другой паре треугольников присутствует только один экстремум. Эта часть фотона и есть вектон или виртуальный фотон (см. Нелипа Н.Ф. "Физика элементарных частиц"). Его максимальная масса не может превышать массу электрона. Фактически, фотон и является несколько преобразованным электроном.

к началу страницы

 

Глюон

y = (xN)(Nx), y = (x(Nx))N

Очень трудно в этой гипотезе найти место глюону. Тем не менее, оно найдено. Хотя, трудности здесь большие... (: кому сейчас легко? :).

Известно, что глюон не имеет массы покоя.

Требуется выполнить два условия:
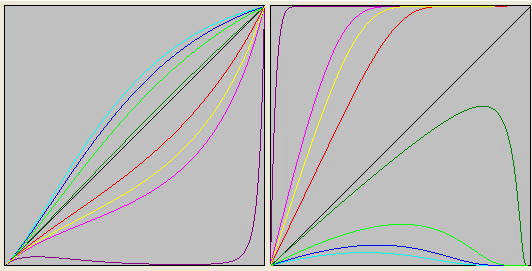
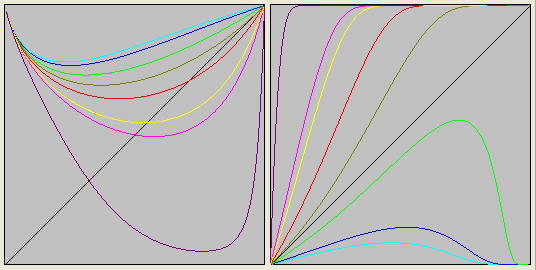
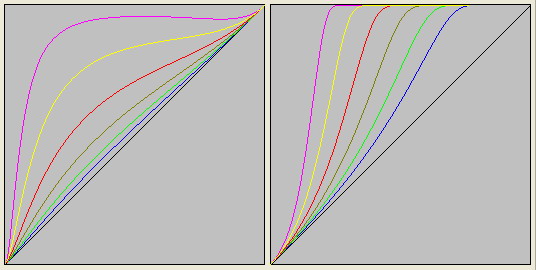
1. Заполнение треугольников должно соответствовать кварку.
2. Безмассовость

Это единственная из всех векторных бозонов функция, не имеющая фиктивной массы. Этот факт, видимо, говорит в пользу "поперечности" глюона.

к началу страницы

 

Глюино и голдстино

y = x((xN)x), y = x((xx)N)

Здесь две идентичные функции представляют сразу две частицы, глюино и голдстино. Функции характеризуются появлением большой фиктивной массы, при достаточно высоких энергиях.

См. Глюино, Голдстоуновский фермион

к началу страницы

 

Голдстоун

y = (xN)(xx) = (x(xx))N

Что можно сказать о голдстоуне, кроме того, что в уравнениях он присутствует.
"Другим следствием спонтанного нарушения симметрии, как и следовало ожидать, является возникновение в лагранжиане безмассового вещественного поля φ₂(x) (голдстоуна).

(Нелипа Н.Ф. "Физика элементарных частиц").

Здесь, в этом случае, не наблюдается никакого намека на фиктивную массу. Это - единственная частица, имеющая "почти вакуумную" характеристику. Неудивительно, что её нельзя так просто "изловить" с помощью наших хитрых "встречных пучков".

к началу страницы

 

Лептокварки: X- и Y-бозоны

Y - бозон

y = x(N(xx))

X - бозон

y = x(N(xN))

Данная функция имеет ярко выраженные свойства векторного бозона и единственное, что отличает её от других, так это наличие большой фиктивной массы. Этим она (функция) схожа с функцией предыдущего Y-бозона , где фиктивная масса подобной величины наблюдается в левом треугольнике.

Смущение вызывает факт неполного заполнения пространства в нижнем треугольнике левой части. Видимо, функции с этим свойством и следует приписать частицу с зарядом 4/3.

Лептокварки:

"Общее название группы гипотеч. элементарных частиц со спином 1, испускание и поглощение к-рых переводит лептоны в кварки или наоборот. ... Масса лептокварков близка к характерной энергии, при которой реализуется великое объединение и чрезвычайно велика (более 10¹⁵ ГэВ)."

к началу страницы

 

Монополь Дирака

y = x(x(NN))

Странная функция, поведение которой похоже на электронную; такая смесь кварка и электрона. Заполняет, в отличие от кварка, не всё пространство треугольника. Вместо этого наблюдается возврат кривой при достижении N = 1/e. Электронная функция таким свойством не обладает.

А что если это и есть монополь Дирака?

Спин магнитного монополя по идее должен равяться 1/2, см. Магнитный монополь.

к началу страницы

 

Максимон

y = x((xN)N)

Почти точное повторение u-Кварка. Частица, имеющая спин 1/2. Максимон?

О максимоне см. здесь или здесь.

к началу страницы

 

Гравитон

y = x((NN)x), y = x((Nx)N)

Известно, что гравитон имеет спин, равный 2. Как это отображено функцией? В правой части ясно виден "распад" графика, показывающий, что данная функция не принадлежит ни к фермионам, ни к скалярным бозонам. Следвательно, она либо векторная, либо тензорная.

Левая часть графика полностью не заполняется в верхнем треугльнике. Это явный факт, который говорит за то, что частица не является векторной.

В правой части также ясно видно, что функция не заполняет всего пространства нижнего треугольника. (У лептокварка, в отличие от гравитона, правая часть заполняется вся). Неполное заполнение в обоих частях, плюс "распадание" графика функции в правой части говорит за то, что это частица со спином 2, т.е. гравитон.

Ясно, что дело на обойдется без "ложки дёгтя". Наличие фиктивной массы в левой части и есть та самая ложка. Это значит, что при высоких энергиях гравитон должен иметь небольшую массу. Но по теории эта частица безмассовая.

Наличие небольшой фиктивной массы также говорит о каком-то "дальнем родстве" с функциями промежуточных бозонов (W и Z).

к началу страницы

 

Гравитино

y = x(N(Nx))

Это полная противоположность предыдущему гравитону. Гравитон, вывернутый на левую сторону.

Мысленно переверните его график. Разве он не похож на гравитон?

Идентичное заполнение пространства в правой части, почти точно копирует гравитон (в левой части). Левая же часть заполняется так же идентично, но в левой части графика гравитино отсутствует распад. Здесь заполнение пространства левой части напоминает заполнение функцией нейтрино. Но если нейтрино дополняет электрон, то гравитино как бы повторяет гравитон.

Характер заполнения пространства в левой части накладывает условие возможного наличия фиктивной массы (достигающей массы электрона).

См. Гравитино: "При нарушении суперсимметрии, гравитино приобретает массу. Величина этой массы является важным феноменологич. параметром во многих суперсимметричных моделях великого объединения."

к началу страницы

 

Хиггсовый бозон

y = (xx)N = (xN)x

Ну, здесь не могу сказать ничего умного, поскольку не знаю о Хиггсе ничего, кроме того, что он имеет массу. :)

Хиггс представлен пятью типами кривых, имеющих похожие свойства.

y = ((xx)x)N = ((xx)N)x = ((xN)x)x

Ещё один Хиггс. Возможно, это две разных частицы, одна из которых представлена двумя, а другая, тремя вырожденными функциями.

y = (xN)(xN), y = (x(xN))N

И ещё один, "поперечный" Хиггс.

Всего в первом поколении 12 скалярных функций, соответствующих 5 частицам, имеющим массу и нулевой спин.

к началу страницы